Kilomeetrid ja miilid, mängud tikkudega ja küülikukasvatus

Küllap saab millalgi mahti tulevase drakoonilise aasta peale ka mõelda, aga selles kirjatükis üritan vahelduseks tegelda matemaatikaga.
Ehk on nii mõnelgi tulnud anglo-ameerika raamatuid lugedes kohtuda probleemiga ,kus mõni asi on väljendatud miilides. Eriti pakiline vajadus võib teisendamise järele tekkida siis, kui sõidate kusagil ameerika kiirteel ja spidomeeter on kalibreeritud km / h peale.
( PS!Otse loomulikult on olemas google ja sellesse tippides näiteks 30 miles in km teeb 49,28032 km.
Sealt saab ka kalkulaatori jaoks konversiooniteguri – 1 miles in km 1.609344
Kui tahate kohe vastavaid tabeleid, siis aitab sait Nii et kõigest praktilisuse viigilehest hoolimata on probleem siiski teoreetiline. )
Oletame siiski, et sõidate ameerika kiirteel, teil ei ole kalkulaatorit ja peate kiiresti hindama, mis kiirusega peate sõitma, kui kiiruse piiranguks on 50 mph.
Selgub, et ühe Itaalia küülikukasvataja Fibonacci kasutuselevõetud jada aitab selle ülesande lahendamisel väga hästi.
Alustada tuleb arvudest 1,1,2 ja arvutada edasi nii: iga järgmine jada liige on eelmise kahe summa.
Saame jada 1, 1,2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ...
Kuid nüüd tahate mingit arvu, näiteks 50 miili teisendada kilomeetriteks, siis esitate selle arvu Fibonacci arvude summana. Loodetavasti ei jõua kiuslik lugeja selleni, et küsida, kas seda mitmel viisil teha ei anna. Saab küll, aga tuleb valida selline, kus puuduksid kaks järjestikust jada liiget (sest kaks järjestikust tuleks asendada hoopis nendele järgneva liikmega.). Piisab, kui esimeseks kandidaadiks võtta kogu aeg kõige suurem Fibonacci arv, mis veel ei ületa esitatavat.
Nii et 50 = 34 + 13 + 3 selles esituses.
Nüüd 50 miilideks saamiseks tuleb iga liidetava asemele võtta lihtsalt JÄRGNEV arv selles jadas:
50 miili = 55 + 21 + 5 = 81 kilomeetrit.
Ütlen ausalt, see meetod ei ole eriti täpne, eksimus on kusagil 0.5 – 1 %, meetod tikub kilomeetritega veidi üle pakkuma, aga peastarvutamiseks sobib suurepäraselt. Ja muudel juhtudele vt. ülaltoodud õpetusi.
Vahest on vastiku konversiooniteguriga jagamine veelgi tülikam, nii on kilomeetritest miilide tagasissaamine koguni asjalikum:
80 = 55 + 21 +3 ( viimane 1 võiks teiseneda 0 –ks, mitte 1-ks )
Järelikult 80 km = 34 + 13 +2 = 49 miili.
Mäng tikkudega
Kui Teile Ameerika viisat mingitel põhjustel ei anta või on lihtsalt lennupiletiks liialt vähe raha, ja ingiskeelses kirjanduses ka miilide ja kilomeetrite vahekord eriti ei huvita, võib Fibonacci arvudest ikkagi kasu olla, isegi siis, kui te pole küülikukasvataja.
Võite näiteks mängida järgmist mängu tikkudega:
Kahes kuhjas on vastavalt n ja m tikku.
Kuhjadest võib eemaldada kas a) ühest kuhjast suvaline arv tikke
b) mõlemast kuhjast võrdne arv tikke
Võidab see, kes võtab viimase tiku (kes naerab viimasena).
Veidi järele mõeldes taipate kohe, et seis (1,2) on teile päris lootusetu.
Vedi veel mõeldes veendute kiiresti, et nüüd iga teine seis, kus ühes kuhjas on kas 1 või 2 tikku (teises suvaline arv, v.a. 1 /2), on võiduseis. (1, k ) seisust saadakse seis (1,2) ja (2,k) seisus (2,1), igast seisust kujul (k,k+1) aga (1,2), kui k tikku mõlemast maha lahutada.
Selles mängus viike ei tule, tikkude arv muudkui kahaneb, keegi ükskord võidab niikuinii.
Järelikult iga seisu kohta peaks saama öelda, kas ta on võiduseis või kaotusseis. Tasuks hakata aga uurima väikseimate tikkude arvudega seise ja sealt ülespoole ronima.
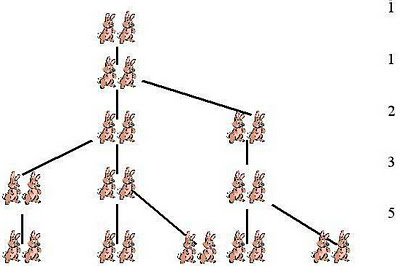
Nii jääb esimesena silma seis (3,5), vahega 2. See on teine kaotusseis, sest iga käigu järel saab vastane järgmisel käigul seisuks (1,2).
Võtame mõlemast kuhjast ühepalju, saame kas (2,4), (1,3) mis taandub (2,1) .
Ka ühest kuhjast võttes tuleb sama tulem.
Edasi on selge, et k,k+2 taandub seisule (3,5), samuti kõik seisud (3,x) või (5,x)
Järgmise kaotusseisu vaheks peab niisiis olema 3. Kandidaadiks sobiks (4,7).
Ka siin veendub kergesti, et vilunud mängija saavutab suvalise käigu järel seisust (4,7) kas seisu (3,5), (1,2) või võidab kohe (kui meeleheitel mängija näiteks ühe kuhja eemaldab).
Edasine analüüs viib kiiresti järgmiste kaotusseisude loetelule.
1. (1,2)
2. (3,5)
3. (4,7)
4. (6,10)
5. (8,13)
.......................
Meetod jätkamiseks on selge, naturaalarvude reas kriipsutage kõik kasutatud arvud läbi, otsige üles järgmine vähim vahega n paar naturaalarve (6 –ndaks kaotusseisuks tuleks 9,15, etc...).
Kuid suurte arvude puhul läheb see kalkuleerimine tülikaks. Mida teha, kui vastane pakub seisuks (500, 1000)?
Tuleb välja, et miilidest kilomeetriteks teisendamise tabel Fibonacci meetodi järgi tegelikult annabki ühtlasi välja kõik kaotusseisud.
(1,2), (3.5), (4,7) on kõik ilusti olemas, ainult et seisu (5,8) ei ole kaotusseis – vastane võtab suuremast kuhjast 5 ära, jääb seis (3,5).
Mis siis määrab seisu tulemi? Selleks kehtib lihtne reegel – määrake antud arvu
lahutusel Fibonacci arvude summaks kõige väiksem arv.
Selle arvu järjenumber Fibonacci jadas ütleb, kas tegemist on kaotusseisu teise või esimese arvuga.
Kui väikseima liidetava järjenumber on paarisarvuline liige Fibonacci jadast (F2, F4, F6 ...., s.t. 1,3,8,21,55,144,377, ...), siis on see arv alati kaotusseisu esimene, s.t. väiksem arv.
Kui väikseima liidetava fibonacci järjenumber on paaritu arv fibonacci jadast (F3,F5.... , s.t. 2,5,13,34,89,233,610...), on see alati kaotusseisu suurem arv.
Näiteid:
I Olgu meil seis (20,30)
20 = 13 + 5 + 2, s.t. peab olema kaotusseisu VIIMANE, mitte esimene arv.
Järelikult peaksime tegelema esimese arvu otsimisega, s.t. teisendama kilomeetrid miilideks Fibonacci meetodil.
Saame 20 km = 8 + 3 + 1 = 12 miili, s.t. kaotusseis on (12,20).
Võitev algus: 30-st tuleb võtta ära 18 tikku. Edasi jätkata samas vaimus.
II (100,161) 100 = 89 + 8 + 3, teiseks selle kaotusseisu arvuks tuleks 162 =144 +13 + 5
161 on ka kaotusseisu esimene arv (144 + 13 + 3 + 1 ), nii et 100-st lahutades ei saa ka võitu.
Mõlemast tuleks niisiis lahutada mingi arv. Võiks sobida 98 = 89 + 8 + 1 (mitte 89 + 8 + 2) , millele vastaks teise arvuna 159 = 144 + 13 + 2 , s.t. mõlemast kuhjast võiks lahutada 2 tikku. Selliste lahendite leidmine ongi kõige raskem, nii et kui olete kaotusseisus, on kõige targem ühest või teisest kuhjast vähendada tikke 1-5 võrra, nii et tekiks vajadus mõlemast kuhjast midagi maha võtta).
Arvude esitamine fibosüsteemis
Selgub, et seda jada saab kasutada ka kodeerimisel. Iga arvu saab esitada 0-de ja 1-de jadana, nii et ei esine iial kahte järjestikust 1 - , s.t. paari 11.
1 = 1
2 = 10
3 = 100
4 = 101
5 = 1000
6 = 1001
...
Selles kummalises arvusüsteemis on miilidest kilomeetrite saamine kõige lihtsam asi – tuleb arvule fibosüsteemis lihtsalt 0 otsa kirjutada. Täpsemalt on see siiski korrutamine kuldlõike arvuga 1.618 ...
Kaotusseis 6, 10 kirjutatakse fibosüsteemis üles nii:
(1001,10010)
Kahjuks ei ole muus elus see süsteem eriti praktiline, nii et pikemalt ma sellel ei peatu.


